Casper CBC

What is CBC : Correct-by-Construction?

In an earlier post we saw how consensus protocols form the very fundamentals of blockchains where independent nodes validate transactions on the network, i.e. the very basic concept of decentralized ledgers. There are then two critical security properties that we must consider for any consensus protocol: safety and liveness.

Safety: A protocol is safe if it will not make inconsistent decisions

Liveness: A protocol is live if it is guaranteed to eventually make a decision

It turns out that ensuring both safety and liveness in a Proof-of-Stake decentralized network is not easy. One of the first attempts to address these issues was called Casper CBC (correct-by-construction). This blockchain architecture provided a groundbreaking framework to address safety, though not liveness. We will see in a later post how more recent research from CasperLabs has helped to address the liveness issue.

The Casper CBC framework describes a family of consensus protocols where each member satisfies a particular safety proof; given some preconditions, all node decisions will be consistent. Each protocol is identified by a number of parameters (properties). The CBC framework captures the relationship between parameters and protocol states through an iterative process. The aim then is to generate a family protocols and to have the ability to make changes to them without losing or having to re-prove properties of the protocol such as safety.

How does the CBC framework work?

Typically, systems are built with rigorous testing in place to validate correctness (eg, unit, system, integration tests etc). The CBC approach is different in that as opposed to testing a predefined system, first principles and rules are put in place, through which correctness is derived. The properties of the system will therefore always be correct. In this way a general protocol space can be defined, and every additional refinement on this can be built and assumed to be correct without the need to test for correctness or the chance that it is incorrect.

If we define a Space S (which can represent the totality of consensus mechanisms), there will be a subspace within this which will define specific mechanisms that use the longest fork chain rule for example. A property P, as defined within the main space can be considered correct throughout the space. However a property P’ defined specifically to be correct within Space S’, will not necessarily be correct for any part of the space outside of S’.

Defining where the Space lives, is the initial problem. Once this is in place the act of the exchange of messages between network validators, grows the network. We can consider it as the initial Space S being defined, and then refinements in the future further defining subspaces.

Below, we will illustrate how the CBC framework’s proof of safety is derived. A thorough proof is omitted however please feel free to read through the original paper here.

Thinking about a consensus protocol in terms of states and state transitions

We can consider the CBC framework in terms of protocol states (sets of messages) and protocol state transitions that clients running the protocol will execute (by receiving messages from consensus forming nodes). Recall that validators are nodes in the decentralized network. When validators ‘speak’, arguments are passed between validators in messages, where a message is comprised of the following 3 key parts:

1. The consensus value
2. The sender (specific validator)
3. Reference to some protocol state (the justification) – important due to the possibility of delayed timings between two messages sent instantaneously. Since there is the possibility of messages getting ‘muddled’, a reference must be in place linking the message to an earlier protocol state in which it is building on.

A present protocol state can therefore be considered as the series of messages. States evolve and one state follows another if the preceding state contains all the messages of the current state.

We next come to the concept of a common future state. This is where there are multiple nodes (validators) with consistent justifications in the messages such that there is a future state agreed. If for example, there exists a validator without this, they will be equivocated by the other validator. You will note here that there is a threshold where if the number of equivocates is below this limit, then a common future will exist. When the common value is reached agents then will not be allowed to decide what is true. This is the safety guarantee and does not permit the consensus to be multiple differing values, this being the principal of the safety guarantee. A property is decided at some state if it is true in all future states. We can further illustrate this with the below several steps.

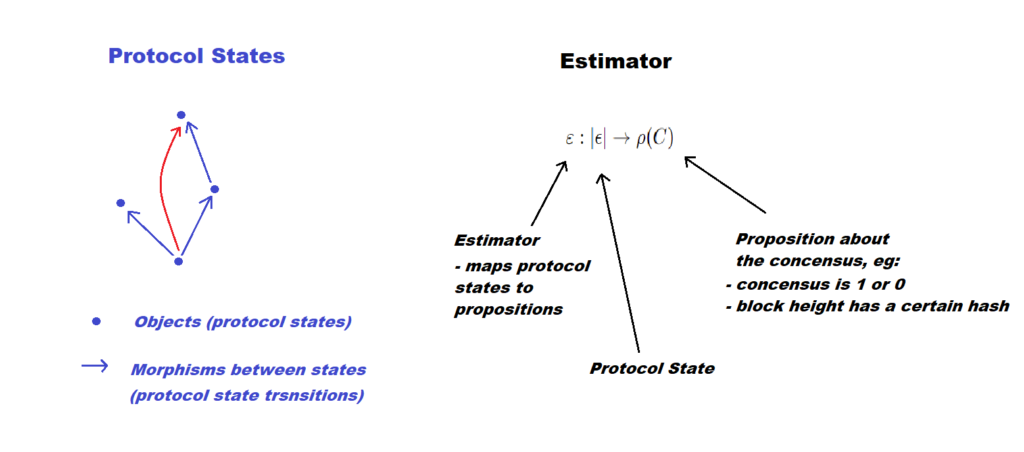
Above (above left) is a diagram showing us this concept of protocol states and the transition between these. We can further define an ‘estimator’ (above right) that maps protocol states (as defined above left) to the propositions about the consensus (for example, an assertion that the block height has a certain hash). The value the estimator implies can be considered safe based upon the following:

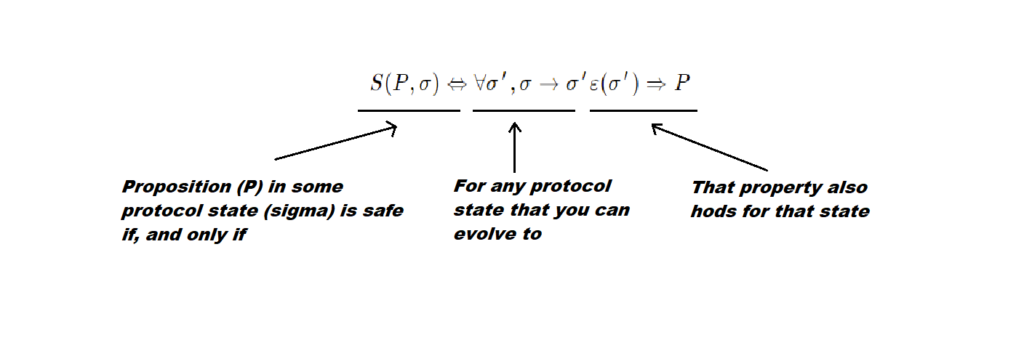
So the value of the estimator (or something the estimator implies) is safe if, for any future protocol state, that value holds. So for example if a block of height 10 has hash XYZ at this protocol state and all future protocol states, then we call the proposition of the block at height 10 with hash XYZ, ‘safe’.

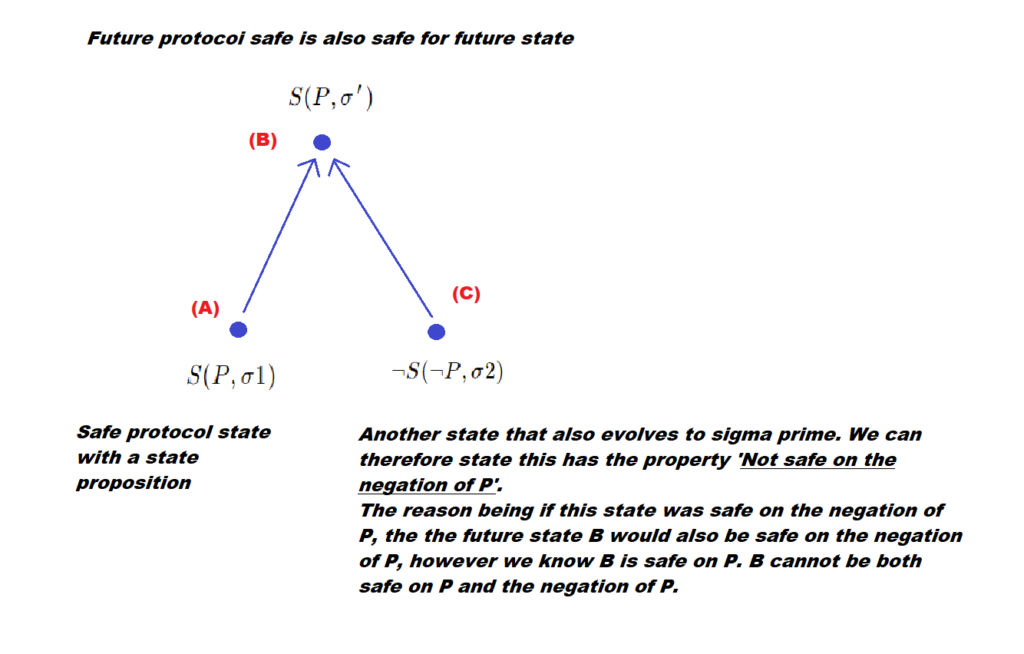
We then think about the common future state. In the above example P and not P cannot exist on the same state therefore both cannot be “consistent”, i.e true on the same state. This is the principal of consensus safety: if two states (sigmas) have a common protocol future you cannot have safety on P on sigma1 and not P on sigma2. Decisions are going to be consensus safe for any two sigmas which have a common protocol future. Any decisions that are invariant over respective futures made by two protocol states (which share a common future protocol state) have to be consistent because of the shared future protocol state. You can see how this bridges the gap from a local notion of safety on a node level to a distributed notion.

Byzantine fault tolerance (BFT) and guarantees of a common protocol future

Before we proceed to discussing the trivial nature of guaranteeing common protocol futures, we should explain briefly the concept of Byzantine faults.

Byzantine fault tolerance (BFT) is the property of a system that is able to resist the class of failures derived from the Byzantine Generals’ Problem. This means that a BFT system is able to continue operating even if some of the nodes fail or act maliciously. At some points in consensus protocols, nodes will become bivalent and committed on a value. It is possible with 100% Byzantine faults for Figure 1 below to happen, with one path being safe on 0 and the other being safe on 1 – however they will not exhibit consensus safety. This is a failure in local safety.

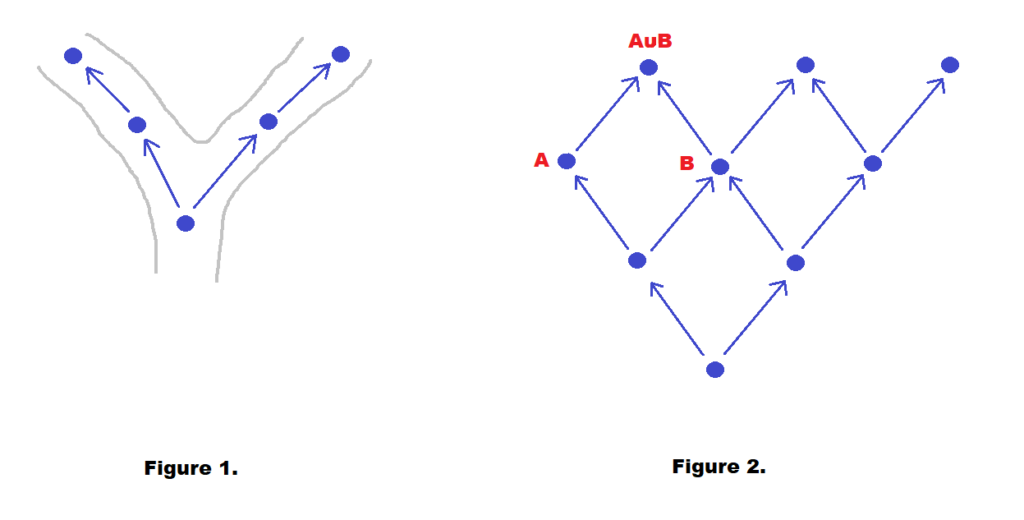
Figure 2. shows protocol states and protocol transitions a within lattice form. In this case we can consider protocol state and states transitions to be:

1. Protocol states – sets of protocol messages
2. State transitions – where receiving a protocol message

i.e. nodes messaging one another. Since 2 nodes can always send messages to each other, we can guarantee that nodes will have a common future for a goal state. The common protocol state in the future for node A and B will therefore be A union B. Therefore in guaranteeing we have a common protocol future, we have also guaranteed consensus safety. However as every 2 states have a common protocol future, we are never able to result in Figure 1 above – which is what you need to make inconsistent, irreversible decisions (non-triviality). Therefore an alteration is made such that any future protocol state which has a number of Byzantine faults above a predefined threshold ‘t’, we delete. Therefore a pair of nodes have a common future state as long as there does not exist >t faults.

The above relies on being able to conduct Byzantine fault detection from a set of 2 message. We shall explore this below.

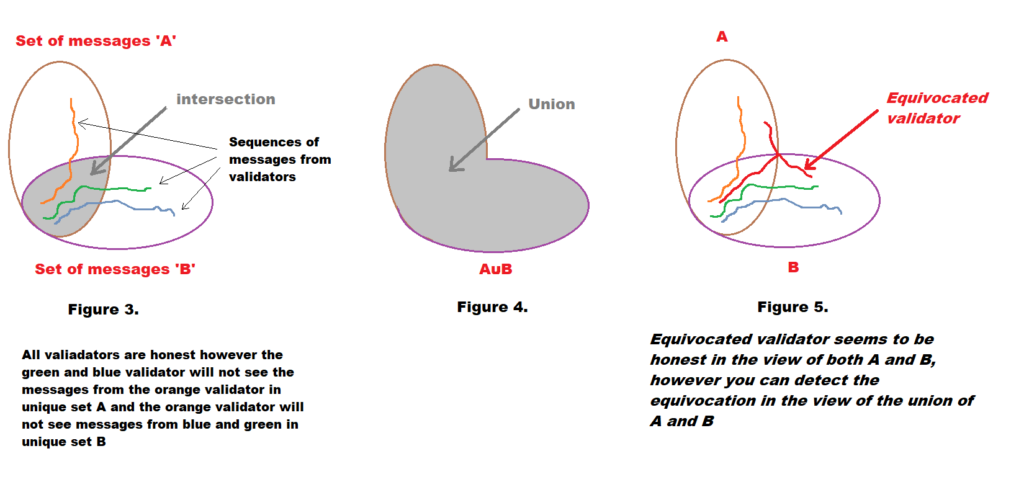
Within figure 3 above we can see two defined sets of messages A and B. These have both an intersect (figure 3), and a union (figure 4). Sequences of messages from validators can be seen as the coloured threads within these sets

Figure 1 would share a common protocol future, however in figure 3 (with the introduction of the red thread), A and B both seem to be honest, however in the union of their views you can detect that the red thread has equivocated and therefore with a threshold set to 0, this would be rejected, as B would not be able to see the part of the red thread in A and vica versa.

Conclusion

As we have seen above, the Casper CBC framework provides a powerful way to develop a family “correct-by-construction” consensus protocols that each share the same proof of Byzantine-fault-tolerant consensus safety, allowing refinements and improvements without needing to re-prove safety each time. At a time when Proof-of-Stake blockchain architectures did not have solid foundations of safety and liveness, this research paved the way for at least satisfying the first of these two critical features.

We will hopefully see in a later post how more recent research from CasperLabs has helped to address both the liveness issue, as well as a number of important improvements to (i) enable the network to reach higher thresholds of finality and (ii) to achieve greater flexibility in how nodes can define their own thresholds of finality for each era.

Disclaimer: This article is written for the purposes of research and does not constitute financial advice or a recommendation to buy.

Stake your CSPR with us at GHOST:
1. Earn passive interest compounded every 2 hours!
2. High performance server with low CPU utilization that can be monitored in real time here
3. Low fees with a GUARANTEE of no increases EVER!
find out more here